GEOMETRY
Geometry is a part of mathematics concerned with questions of size, shape, and relative position of figures and with properties of space. Geometry is one of the oldest sciences.
USES : How much concrete is needed for a footing with these dimensions?, or how much fencing is needed to enclose the region in this sketch. Carpentry generally does not require much formal education, but some of their applicants thought all they had to do was show up.
Geometry being used in :
(a) Computer graphics is based on geometry - how images are transformed when viewed in various ways.
(b) Computer-aided design, computer-aided geometric design. Representing shapes in computers, and using these descriptions to create images, to instruct people or machines to build the shapes, etc. (e.g. the hood of a car, the overlay of parts in a building construction, even parts of computer animation).
(c) Robotics. Robotic vision, planning how to grasp a shape with a robot arm, or how to move a large shape without collission.
(d) Medical imaging - how to reconstruct the shape of a tumor from CAT scans, and other medical measurements. Lots of new geometry and other math was (and still is being) developed for this.
(e) Structural engineering. What shapes are rigid or flexible, how they respond to forces and stresses. Statics (resolution of forces) is essentially geometry. This goes over into all levels of design, form, and function of many things. I have attended some interesting architecture and design conferences where all of this flows together - sometimes (in North American culture) with people knowing too little geometry to do some of the things well.
(f) Protein modeling. Much of the function of a protein is determined by its shape and how the pieces move. Mad Cow Disease is caused by the introduction of a 'shape' into the brain (a shape carried by a protein). Many drugs are designed to change the shape or motions of a protein - something that we are just now working to model, even approximately, in computers, using geometry and related areas (combinatorics, topology).
(g) Physics, chemistry, biology, .... . Symmetry is a central concept of many studies in science - and also the central concept of modern studies of geometry. Students struggle in university science if they are not able to detect symmetries of an object (molecule in stereo chemistry, systems of laws in physics, ... ). the study of transfromations and related symmetries has been, since 1870s the defining characteristic of geometric studies.
Picture of Geometry used in the real world
Geometry is used everywhere. Everywhere in the world there is geometry, mostly made by man. Most man made structures today are in a form of Geometric. How, you ask? Well some examples would the a CD, that is a 3-D circle and the case would be a rectangular prism. Buildings, cars, rockets, planes, maps are all great examples.
Here's an example on how the world uses Geometry in buildings and structure :-
 1. This a pictures with some basic geometric structures. This is a modern reconstruction of the English Wigwam. As you can there the door way is a rectangle, and the wooden panels on the side of the house are made up of planes and lines. Except for really planes can go on forever. The panels are also shaped in the shape of squares. The house itself is half a cylinder.
1. This a pictures with some basic geometric structures. This is a modern reconstruction of the English Wigwam. As you can there the door way is a rectangle, and the wooden panels on the side of the house are made up of planes and lines. Except for really planes can go on forever. The panels are also shaped in the shape of squares. The house itself is half a cylinder.
 2. Here is another modern reconstruction if of a English Wigwam. This house is much similar to the one before. It used a rectangle as a doorway, which is marked with the right angles. The house was made with sticks which was straight lines at one point. With the sticks in place they form squares when they intercepts. This English Wigwam is also half a cylinder.
2. Here is another modern reconstruction if of a English Wigwam. This house is much similar to the one before. It used a rectangle as a doorway, which is marked with the right angles. The house was made with sticks which was straight lines at one point. With the sticks in place they form squares when they intercepts. This English Wigwam is also half a cylinder.

 3. This is a modern day skyscraper at MIT. The openings and windows are all made up of parallelograms. Much of them are rectangles and squares. This is a parallelogram kind of building.
3. This is a modern day skyscraper at MIT. The openings and windows are all made up of parallelograms. Much of them are rectangles and squares. This is a parallelogram kind of building.
 4. This is the Hancock Tower, in Chicago. With this image, we can show you more 3D shapes. As you can see the tower is formed by a large cube. The windows are parallelogram. The other structure is made up of a cone. There is a point at the top where all the sides meet, and There is a base for it also which makes it a cone.
4. This is the Hancock Tower, in Chicago. With this image, we can show you more 3D shapes. As you can see the tower is formed by a large cube. The windows are parallelogram. The other structure is made up of a cone. There is a point at the top where all the sides meet, and There is a base for it also which makes it a cone.
 5. This is another building at MIT. this building is made up of cubes, squares and a sphere. The cube is the main building and the squares are the windows. The doorways are rectangle, like always. On this building There is a structure on the room that is made up of a sphere.
5. This is another building at MIT. this building is made up of cubes, squares and a sphere. The cube is the main building and the squares are the windows. The doorways are rectangle, like always. On this building There is a structure on the room that is made up of a sphere.
 6. This is the Pyramids, in Indianapolis. The pyramids are made up of pyramids, of course, and squares. There are also many 3D geometric shapes in these pyramids. The building itself is made up of a pyramid, the windows a made up of tinted squares, and the borders of the outside walls and windows are made up of 3D geometric shapes.
6. This is the Pyramids, in Indianapolis. The pyramids are made up of pyramids, of course, and squares. There are also many 3D geometric shapes in these pyramids. The building itself is made up of a pyramid, the windows a made up of tinted squares, and the borders of the outside walls and windows are made up of 3D geometric shapes.
 7. This is a Chevrolet SSR Roadster Pickup. This car is built with geometry. The wheels and lights are circles, the doors are rectangular prisms, the main area for a person to drive and sit in it a half a sphere with the sides chopped off which makes it 1/4 of a sphere. If a person would look very closely the person would see a lot more shapes in the car. Too many to list.
7. This is a Chevrolet SSR Roadster Pickup. This car is built with geometry. The wheels and lights are circles, the doors are rectangular prisms, the main area for a person to drive and sit in it a half a sphere with the sides chopped off which makes it 1/4 of a sphere. If a person would look very closely the person would see a lot more shapes in the car. Too many to list.
Symmetry
Symmetry in common usage generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically-pleasing proportionality and balance; such that it reflects beauty or perfection. The second meaning is a precise and well-defined concept of balance or "patterned self-similarity" that can be demonstrated or proved according to the rules of a formal system: by geometry, through physics or otherwise.
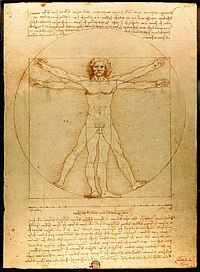 Leonardo da Vinci's Vitruvian Man (1492) is often used as a representation of symmetry in the human body and, by extension, the natural universe.
Leonardo da Vinci's Vitruvian Man (1492) is often used as a representation of symmetry in the human body and, by extension, the natural universe.
Reflection symmetry,
Rotational symmetry is symmetry with respect to some or all rotations in m-dimensional Euclidean space
Helical symmetry is the kind of symmetry seen in such everyday objects as springs, Slinky toys, drill bits, and augers. It can be thought of as rotational symmetry along with translation along the axis of rotation, the screw axis).
Symmetry in religious symbols
Symmetry in architecture (Eg. Qutub Minar, etc)