How will you measure if the challenge is diminishing, or the student is becoming more successful?
♦If the student does not yet have an IEP in which to measure progress against, I will create SMART goals, possibly with the help of a special education teacher.
Target setting and IEPs for Numeracy
When target setting, it is vital that the specific area of difficulty is identified and SMART targets are written. (Specific, Measurable, Achievable, Realistic and Time limited).
-
Targets should be based on diagnostic assessment which includes individual skills, structures and learning style
- Targets should be shared and agreed with learners and parents/caregivers
- Target setting for numeracy should consider the widest range of focus areas in order to address progress
- Evaluation of targets should be based upon the learners response to the teaching methods, approaches and measurable progress made in the specific focus area

♦I will also have the student track his own progress of math fluency over time which I think helps with accountability and increasing his confidence and perception of achievement.
♦I think that day-to-day assessments of math lessons will be the starting point - noting the student's errors and misconceptions. From that data, I hope to find the areas in which targeted interventions could be implemented, and rate and assess the student's current "level" in the learning of mathematics.
“Level” is not used in relation to describe the difficulty of the mathematical topic or focus. Based on the work by Sharma (1990), the term “level” refers to the order that information presented mathematically is processed and learned. (DfES, 2001)
Levels of Learning
This hierarchy of learning can in turn offer a structure for the teacher to follow. Sharma proposes the following order as effective for the teaching of mathematics to pupils with dyslexia:
Intuitive: At the intuitive level, new material is connected to already existing knowledge. (The teacher checks out the connection is correct).
Concrete/Experiential: Apparatus, materials are used to introduce, practise and re-enforce rules, concepts and ideas.
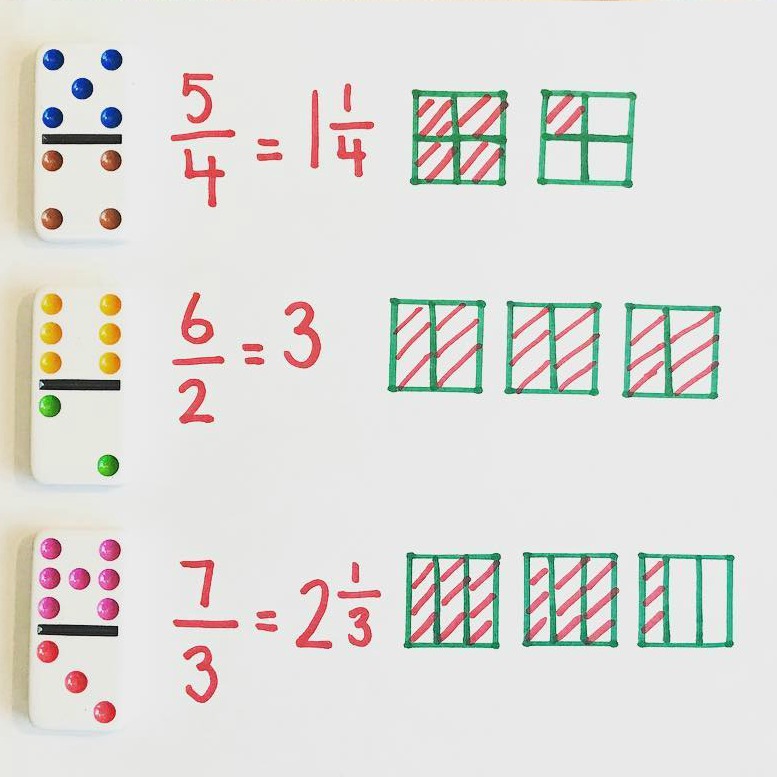
Pictorial/Representational: Picture, diagram, image is used to solve a problem or prove a theorem.
Abstract: Student is able to process symbols and formulae.
Applications: Student is able to apply a previously learned concept to another topic.
Communication: The student is able to convey knowledge to another pupil reflecting an embedded understanding and the highest level of learning.
Assessing Mastery
The term “level” refers to the order that information presented mathematically is processed and learned. Mahesh C. Sharma, in “Learning Problems in Mathematics: Diagnostic and Remedial Perspectives” states that “almost all mathematics teaching activities, in most classrooms, take place at the abstract level. That is where most textbooks are; that is where most of the tests and examinations are.” For students who have not mastered particular math content, he proposes the following order or “Levels of Math” as effective for teaching mathematics: intuitive, concrete/experiential, pictorial/representational, abstract, applications, and communication.
The chart below explains each level and gives an example of what that level would look like in the classroom:
Levels Explanation Example
|
Intuitive |
At the intuitive level, new material is connected to already existing knowledge. (The teacher checks that the connection is correct.) Introduce each new fact or concept as an extension of something the student already knows. |
When a student is given three-dimensional circles cut into fractional pieces, he/she intuitively begin to arrange them into complete circles, thus seeing the wedges as part of a whole.  |
|
Concrete/ Experiential |
Manipulitives are used to introduce, practice and re-enforce rules, concepts, and ideas. Present every new fact or concept through a concrete model. Encourage students to continue exploring through asking other questions. |
Using the concrete model (in this case the wedges) helps the student learn the fractional names. As the student names the pieces, the instructors asks questions such as, “How many pieces are needed to complete the circle? Yes, four, so one out of these four is one fourth of the circle. As students continue to explore they may see that two of the quarters equal half the circle.
|
|
Pictorial/ Representational |
Picture, diagram, image is used to solve a problem or prove a theorem. Sketch or illustrate a model of the new math fact. Pictorial models are those pictures often provided in textbook worksheets. |
When the student has experienced how some pieces actually fit into the whole, present the relationship in a pictorial model, such as a worksheet.
|
|
Abstract |
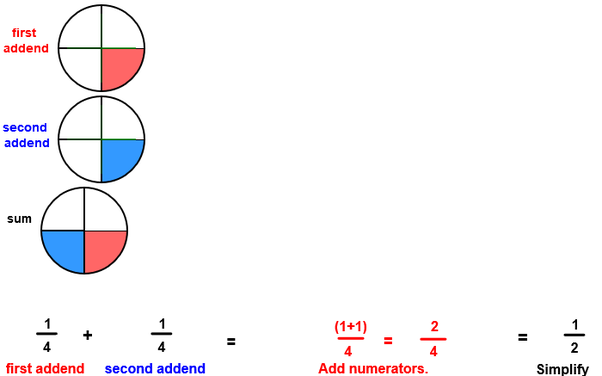
Student is able to process symbols and formulae. Show students the new fact in symbolic (numerical) form. |
After the student has the concrete and pictorial models to relate to, he can understand that 1/4 + 1/4 is not 2/8. Until this concept has been developed, the written fraction is meaningless to the student. |
|
Applications |
Student is able to apply a previously learned concept to another topic. Ask student to apply the concept to a real-life situation. The student can now approach fractions with an understanding that each fraction is a particular part of a whole. The instructor can now introduce word problems without illustrations because students have images in their heads.
|
A student who is asked to give a real-life example or situation might respond with 1/4 cup of flour + 1/4 cup of flour equals 1/2 cup of flour .
|
|
Communication |
The student is able to convey knowledge to another student reflecting an embedded understanding and the highest level of learning. The student’s success in this task reflects an embedded understanding and the highest level of learning.
|
Ask students to convey their knowledge to other students, i.e., students must translate their understanding into their own words to express what they know. |
Next Steps and Strategies
►The DfES strategy guide then recommends using grade-level milestone checklists to “track back” to find the error or misconception appropriate for the child irrespective of the year group.
►Based on their errors and misconceptions, I will use targeted resources, key vocabulary, and teaching activities for intervention.
►Diagnostic assessments such as standardized tests can then be used for diagnostic purposes but they will also give an approximate mathematics age for each student.
References:
British Dyslexia Association describes Dyscalculia. (2001). Dyscalculia. http://www.mathematicshed.com/uploads/1/2/5/7/12572836/guidance_dyscalculia.pdf
Massachusetts Adult Basic Education Curriculum Framework, Massachusetts Department of Education, Adult and Community Learning Services, October 2005.
Mahesh C. Sharma, Handout entitled, “Learning Problems in Mathematics: Diagnostic and Remedial Perspectives.”